Problemas Matemáticos e a Interface com outras Áreas do Conhecimento

Problemas Matemáticos e a Interface com outras áreas do Conhecimento


Isto é Show de Bola. Participe!!!!!!





10.) Um operário ganha R$ 3,00 por hora de trabalho de sua jornada semanal regular de trabalho, que é de 40 horas. Eventuais horas extras são pagas com um acréscimo de 50%. Encontre uma fórmula algébrica para expressar seu salário bruto semanal, S, para as semanas em que trabalhar h horas, com .

11.) Além do custo administrativo fixo, diário, de R$ 500,00, o custo da produção de x unidades de certo item é R$ 2,50 por unidades. Durante o mês de maio, o custo total da produção variou entre o máximo de R$ 1.325,00 e o mínimo de R$ 1.200,00 por dia. Quais foram os níveis de produção máximo e mínimo durante esse mês?

12.) O empregado de uma empresa ganha mensalmente x reais. Sabe-se que ele paga de aluguel R$ 120,00 e gasta 3/4 de seu salário em sua manutenção, poupando o restante. Então:

a) Encontre uma expressão matemática que defina a poupança P em função de seu salário x.

b) Para poupar R$ 240,00, qual deverá ser o seu salário mensal?

13.) Tem-se, abaixo, parte da tabela de preços da postagem de cartas em uma Agência dos Correios.

Verifique se são verdadeiras ou falsas. Nessa agência:

a) Para postar duas cartas, com peso de 25 g e 12 g, deve-se pagar R$ 2,70.

b) Para postar três cartas, com peso de 10 g, 30 g e 45 g, deve-se gastar R$ 5,70.

c) Se uma pessoa pagou R$ 3,50 pela postagem de duas cartas, uma delas pode ter pesado 45 g.

d) Paga-se R$ 5,40 para postar três cartas de 32 g cada.

e) A função que ao peso x de uma carta, .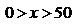

14.) O custo C em reais para produzir x unidades de um componente eletrônico é dado por C(x) = 18x + 4.500.

a) Qual é o custo para se produzir 1.000 unidades desse produto?

b) Quando obtiver um lucro de 20% sobre o valor de custo, qual deverá ser o preço de cada componente eletrônico?

15.) Um vendedor recebe mensalmente um salário composto de duas partes: uma parte fixa, no valor de R$ 900,00, e uma variável, que corresponde a uma comissão de 8% do total de vendas que ele fez durante o mês.

a) Expressar a lei da função que representa seu salário mensal.

b) Calcular o salário do vendedor sabendo que durante um mês ele vendeu R$ 50.000,00 em produtos.

16.) Um botânico mede o crescimento de uma planta, em centímetros, todos os dias. Ligando os pontos, colocados por ele, num gráfico, resulta a figura abaixo. Se mantida, sempre, esta relação entre tempo e altura, que altura a planta terá, no trigésimo dia?

17.) O custo de fabricação de x unidades de um produto é C = 100 + 2x. Cada unidade é vendida pelo preço p = R$ 3,00. Para haver um lucro igual a R$ 1.250,00 devem ser vendidas k unidades. Determine o valor de k.

18.) Depreciação de um carro é a perda de seu valor original (valor do carro de zero quilômetro) em função do tempo. Considere V o valor depreciado do carro após x anos. Uma revendedora usa a lei de uma função polinomial do 1ª grau para calcular V para carros com até 6 anos. Esta agência anunciou um carro com 5 anos de uso por R$ 12.000,00. Esse modelo, quando novo (x = 0), custa R$ 30.000,00.

a) Escreva a lei da função V(x).

b) Qual é o valor depreciado desse carro após 3 anos?

19.) Um móvel se desloca numa rodovia da cidade A para a cidade B, segundo a função s(t) = 100 + 80t, sendo s (espaço) em km e t (tempo) em horas. Sabendo que A está localizada no km 100 desta rodovia e B dista 350 km de A, pede-se:

a) O gráfico da função s

b) A posição do móvel para t = 3 horas

c) Após quanto tempo de viagem o móvel chega ao destino

d) A posição do móvel para t = 0. Explique o significado disto.

20.) Uma cooperativa de avicultura abate, ao custo de R$ 1,00 o quilograma do frango vivo – preço pago ao produtor – e vende-o resfriado a R$ 1,95 – ao atacadista. O investimento inicial para os cooperados foi de R$ 19.000,00. Com base nas informações acima:

a) Escreva as leis da função “custo inicial” e da função “receita”.

b) Represente graficamente as duas funções num mesmo sistema de coordenadas cartesianas, identificando-as.

c) Determine o ponto de intersecção dos gráficos, explicando seu significado matemático.

21.) Um móvel se movimenta com velocidade constante obedecendo á formula matemática s = 40 - 2t, sendo s a posição do móvel, em metros, e t o tempo, em segundos. Construa o gráfico dessa função.

22.) Um vendedor recebe um salário fixo de R$ 300,00 por mês, mais uma comissão de 5% sobre as vendas que excederem a R$ 1.000,00.

a) Denotando por y o salário e por x os valores das vendas no mês, construa o gráfico da função que representa o salário mensal desse vendedor.

b) Qual seria o seu salário em um mês cujas vendas atingiram R$ 1.800,00.

23.) Numa pequena industria, o faturamento liquido relativo a um certo produto é calculado pela formula f(x) = 4x - 1.000, onde f(x) representa o faturamento liquido de x unidades vendidas. Faça um estudo do sinal dessa função e determine a quantidade mínima de unidades que devem ser vendidas para que haja lucro.

24.) O recipiente da figura está completamente cheio com 20 litros de água. Abre-se uma torneira que o esvazia á razão de 2 litros por minuto.

a) Escreva a função que representa o volume de água V que resta no tanque em relação ao tempo T em minutos.

b) Em quanto tempo o tanque ficará vazio?
c) Quais os valores que T pode assumir nessa função?

d) Qual o conjunto imagem dessa função?

25.) Um motorista de táxi cobra, em cada corrida, o valor fixo de R$ 3,20 mais R$ 0,80 por quilômentros rodado.

a) Indicando por x o número de quilômetros rodados e por P o preço a pagar pela corrida, escreva a expressão que relaciona P com x.

b) Determine o número máximo de quilômetros rodados para que, em uma corrida, o preço a ser pago não ultrapasse R$ 120,00.

26.) O custo total da fabricação de determinado artigo dependente do custo de produção, que é de R$ 45,00 por unidade fabricada, mais um custo fixo de R$ 2.000,00. Pede-se:

a) A função que representa o custo total em relação á quantidade fabricada.

b) O custo total da fabricação de 10 unidades.

c) O número de unidades que deverão ser fabricadas para que o custo total seja de R$ 3.800,00.

d) O gráfico da função custo total, destacando os dados obtidos nos itens anteriores.

27.) O dono de uma marcenaria, que fábrica um certo tipo de armário, sabe o número de armário N que ele pode fabricar por mês depende do número X de funcionários trabalhando na marcenaria, e essa dependência é dada pela função N(x) = x² + 2x. Qual é o número de empregados necessário para fabricar 168 armários em um mês?

Note que, na função N(x) = x² + 2x, x representa o número de trabalhadores, sendo, portanto um número natural (0, 1, 2, 3, ...). Então, essa função tem domínio D = N.

Queremos saber qual o valor de x para que N(x) = 168.

28.) Um corpo lançado do solo verticalmente para cima tem posição em função do tempo dada pela função h(t) = 40t - 5t², onde a altura h é dada em metros e o tempo t é dado em segundos. Determine:

a) A altura em que o corpo se encontra em relação ao solo no instante t = 3s.

b) Os instantes em que o corpo esta á uma altura de 60m do solo.

29.) Uma bola é largada do topo de uma torre, caindo na vertical até alcançar o chão. Sua altura, em metros, em relação ao chão, após t segundos de queda, é dada pela função A(t) = -3t² + 432. Baseando-se nessas informações, analise as afirmações abaixo.

a) Após 2 segundos de queda, a bola se encontra a 410 m do chão.

b) A altura da torre é 429 m.

c) A bola atinge o chão ao fim de 12 segundos de queda.

d) Durante o 5° segundo de queda, a bola percorre uma distancia de 27 m.

e) A partir do 7° segundo de queda, a altura da bola em relação ao solo é menor que 189 m.

30.) A temperatura é medida, no Brasil, em graus Celsius (°C). Mas em alguns países, principalmente os de língua inglesa, a temperatura é medida em outra unidade, chamada graus Fahrenheit (°F). Para converter medidas de uma escala para outra, pode-se utilizar a fórmula , onde C é a temperatura medida em graus Celsius e F a temperatura medida em graus Fahrenheit.

a) Em certo dia, o jornal noticiou que a temperatura em Miami era de 62°F. Qual a temperatura equivalente em graus Celsius?

b) A que temperatura, em graus Fahrenheit, equivale a temperatura de 38°C?

c) Qual o equivalente a 0°C em graus Fahrenheit?

31.) Uma vídeolocadora aluga fitas de vídeo no final de semana, cobrando o preço segundo a tabela abaixo.

Veja que o valor a ser pago pelo aluguel das fitas dependente do número de fitas alugadas.

Dizemos que o preço está em função do número de fitas.

O número de fitas alugadas é a variável independente.

O preço a ser pago é variável dependente.

Os valores que é variável independente pode assumir, ou seja, 1,2,3,4..., até o número máximo de fitas disponíveis na locadora, são os elementos do domínio dessa função.

Os preços a serem pagos pelo aluguel são os elementos da imagem dessa função.

Com base na tabela, podemos responder a uma série de questões:

a) Qual o valor a ser pago no aluguel de 6 fitas?

b) Qual será o preço de cada fita no aluguel de 4 fitas?

c) Em relação ao preço de cada fita, qual a porcentagem do desconto que terei se levar 3 fitas?

32.) Suponha que Ana tenha uma corda de 12 m e com ela deseje construir retângulos, onde cada lado é representado por um número inteiro de metros.

a) Dê as medidas dos lados dos possíveis retângulos construídos por Ana.

b) Dentre todos os retângulos, qual deles tem a maior área?

33.) Uma pedra é lançada do solo verticalmente para cima. Ao fim de t segundos, atinge a altura h, dada por h = 40t - 5t²:

a) Calcule a posição da pedra no instante 2 s.

b) Calcule o instante em que a pedra passa pela posição 75 m, durante a subida.

c) Determine a altura máxima que a pedra atinge.

d) Construa o gráfico da função h para .

34.) Um projétil é lançado da origem O (0, 0), segundo um referencial dado, percorre uma trajetória parabólica cuja função representativa é y = ax² + bx. Sabendo que o projétil atinge sua altura máxima no ponto (2, 4), escreva a função dessa trajetória.

35.) Suponha que um grilo, ao saltar do solo, tenha sua posição no espaço descrita em função do tempo (em segundos) pela expressão h(t) = 3t - 3t², onde h é a altura atingida em metros.

a) Em que instante t o grilo retorna ao solo?

b) Qual a altura máxima em metros atingida pelo grilo?

36.) Num parque de diversões, A, quando o preço de ingresso é R$ 10,00, verifica-se que 200 frequentadores comparecem por dia; quando o preço é R$ 15,00, comparecem 180 frequentadores por dia.

a) Admitindo que o preço (p) relaciona-se com o número de frequentadores por dia (x) através de uma função do 1ª grau, obtenha essa função.

b) Num outro parque, B, a relação entre p e x é dada por p = 80 - 0,4x. Qual o preço que deverá ser cobrado para maximizar a receita diária?

37.) Os alunos de uma escola fretaram, para sua viagem de formatura, um avião com capacidade para 200 pessoas. Cada estudante comprometeu-se a pagar R$ 210,00, caso o avião ficasse totalmente cheio. Caso o avião não ficasse cheio, então cada aluno pagaria um adicional de R$ 1,70 por cada lugar que ficasse vazio.

a) Qual a receita obtida se, no dia, comparecerem 160 estudantes?

b) Qual a equação da receita, r, em função do n° x de alunos que irão comparecer? Obs: .

c) Qual valor de x que gera receita máxima?

38.) Na revelação de um filme, uma óptica calcula preço a ser cobrado usando a fórmula P = 12,00 + 0,65n, onde P é o preço, em reais, a ser cobrado e n o número de fotos reveladas do filme.

A fórmula acima nos dá a condição de dependência entre o preço a ser cobrado e o número de fotos reveladas. O preço depende do número de fotos reveladas, ou ainda, o preço é dado em função do número de fotos reveladas.

O número de fotos reveladas é a variável independente.

O preço a ser pago é a variável dependente.

O domínio dessa função é o conjunto dos possíveis números de fotos reveladas. Se for um filme de 24 fotos, o domínio será {0, 1, 2, 3, ..., 24}.

A imagem é o conjunto dos preços a serem pagos.

Algumas questões que podem ser resolvidas a partir da fórmula:

a) Quanto pagarei se forem reveladas 22 fotos do meu filme?

b) Se paguei a quantia de R$ 33,45 pela revelação, qual o total de fotos reveladas?

39.) As trajetórias dos animais saltadores são, normalmente, parabólicas. A figura mostra o salto de uma rã representado num sistema de coordenadas cartesianas. O alcance do salto é de 4 metros e a altura máxima atingida é de 1 metro.

A partir desses dados, determine:

a) A função da trajetória da rã.

b) As coordenadas do vértice.

c) Para quais valores de x a função é crescente ou decrescente.

40.) Durante o processo de tratamento, uma peça de metal sofre uma variação de temperatura descrita pela função . Em que istante t a temperatura atinge seu valor Maximo?

41.) Um agricultor precisa cercar um espaço reservado a uma horta com formato retangular. A cerca para três lados da horta custa R$ 40,00 o metro e a cerca para o quarto lado custa R$ 60,00 o metro. O agricultor dispõe de R$ 720,00 para gastar na cerca. Que dimensões ele deve dar esse espaço para maximizar a sua área?

a) 4,5 m x 3 m

b) 5,4 m x 3 m

c) 4,5 m x 3,6 m

d) 5,4 m x 3,6 m

e) 6,1 m x 3,2 m

42.) Quando uma pizzaria cobra R$ 14,00 por pizza, 80 unidades são vendidas por dia. Quando o preço é R$ 12,00 por pizza, 90 unidades são vendidas.

a) Admitindo que a quantidade vendida (y) seja função do 1ª grau do preço (x), qual o preço que deve ser cobrado para maximizar a receita diária?

b) Se a relação entre y e x fosse y = - 4x + 160, , e o custo de cada pizza R$ 8,00 , qual o preço que deveria ser cobrado para maximizar o lucro?

43.) O consumo (C) de uma família e sua renda (x) são tais que C = 1.000 + 0,6x . Podemos então afirmar que:

a) Se a renda diminui em 1.000, o consumo diminui em 1.600.

b) Se a renda aumenta em 100, o consumo aumenta em 100.

c) Se a renda diminui em 100, o consumo diminui em 100.

d) Se a renda aumenta em 1.000, o consumo aumenta em 600.

e) Se a renda dobra o consumo dobra.

44.) Uma fábrica de bolsas tem um custo fixo mensal de R$ 5. 000,00 . Cada bolsa fabricada custa R$ 25,00 e é vendida por R$ 45,00 . Para que a fábrica tenha um lucro mensal de R$ 4.000,00 , ela deverá fabricar e vender mensalmente x bolsas. Qual o valor de x?